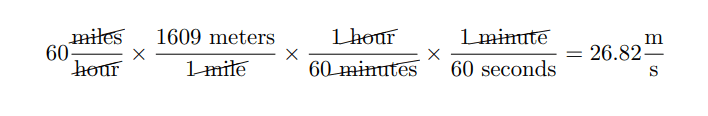Musings of an Old Chemist

A Chemist's Perspective on the Habits and Skills STEM Students Need For Success

Tag: stem

The Grade Illusion: Why High Test Scores Don’t Necessarily Equate With Concept Mastery (And How to Fix It)
If you are an aspiring STEM student, or the parent of one, I want you to consider a terrifying possibility: It is possible to have a 4.0 GPA and know/retain almost nothing.

I saw this contradiction in the students I would tutor. They were bright, hardworking, and ambitious. They had mastered the art of getting the “A.” They knew how to take tests, follow instructions, and allocate their time to receive a high score.

However, if I asked them to apply a physics concept from two weeks before to a new problem assigned that day, they would freeze. Their knowledge of the material (data) was gone.

This is the Grade Illusion. We have built an educational culture – especially in high-stakes fields like STEM, where the “High Score” has become the product. But in the real world, the test scores from high school and college courses are irrelevant. The only thing that matters is mastering the content.

If you want to survive the transition from “A-student” to “successful scientist,” you need to understand how your own mind works. You need to stop renting knowledge and start owning it.

The Knowledge Retention Misconception: RAM vs. Hard Drive

To understand why intelligent students often feel like impostors, we need to examine how the brain stores information.

Think of your brain like a computer. You have two types of storage:
1. RAM (Random Access Memory): This is short-term, high-speed memory storage. It holds the data you need right now. It is volatile; when the power cuts (or the test ends), the data is wiped to make room for the next task.
2. The Hard Drive: This is long-term storage. It is slower to write to, but the data remains there forever, ready to be recalled years later.
The modern educational system encourages you to use your RAM, not your Hard Drive. We call this Cramming, or as we discussed in an earlier blog post, the act of memorization/regurgitation.

When you cram for a calculus midterm, you are loading complex formulas into your RAM. You hold them there—stressfully—for 24 hours. You walk into the exam, dump the RAM onto the paper, and get a 95%. You feel successful.

But 48 hours later, that RAM is cleared to make space for Chemistry. The “Save to Hard Drive” function never happened.

The Science of Forgetting

This isn’t just a metaphor; it is a biological fact. In the late 19th century, psychologist Hermann Ebbinghaus mapped the “Forgetting Curve.”

The curve shows that without deep processing (the struggle necessary to understand something), humans lose roughly 50% of new information within a day and 90% within a week.

The student who crams and gets an “A” peaks at 100% on Tuesday morning. By next Tuesday, their retention dropped to nearly the same level as that of the student who failed. The grade is a record of what you knew for one hour, not what you carry into your career.

From an economics perspective, consider this as the difference between Renting and Owning.
- Cramming is Renting. You pay a high price in stress and sleep deprivation. You get to “live” in the knowledge for a day. But once the test is over, your “lease” is up, and you are evicted. You have zero equity.
- Deep Learning is Owning. You pay a “mortgage” of daily, consistent study. It feels slower. It feels harder. But two years later, when you are designing a load-bearing bridge, for example, that physics principle is yours.
The Illusion of Competence

“But I got an A!” you might argue. “The test says I know the material.”

Does it?

In 1956, in the publication “Taxonomy of Educational Objectives: The Classification of Educational Goals,” a committee of educators chaired by Benjamen Bloom developed a framework to rank levels of understanding called “Bloom’s Taxonomy.”

Shutterstock

Most high school tests—and frankly, many college exams—operate at the bottom three levels: Knowledge (learn the formula), Comprehension (understand when to use the formula), and Application (plug numbers into the formula).

If you are good at memorization, you can ace these tests without ever moving up the pyramid. But a career in STEM fields lives entirely at the top three levels:
- Analysis: Why did the experiment fail?
- Evaluation: Which method is best for this specific application?
- Synthesize (Create): Develop an improved solution that isn’t in the textbook.
The Illusion of Competence

This creates the Illusion of Competence. You have a transcript full of “A’s” that certify you are an expert, but your internal drive has never been stress-tested at the “Analysis” or “Synthesis” level. When you eventually hit a problem that requires those skills, you don’t just struggle—you crash.

The most dangerous side effect of the Grade Illusion isn’t academic; it’s psychological.

The Performance = Identity Misconception

When you spend your entire life chasing the “High Score,” you begin to associate your Performance with your Identity. You believe the equation: My Grade = My Worth.

In STEM, this is lethal. In English class, a grade of “C” might seem subjective. In Physics or Chemistry, a “wrong answer” is objectively wrong. If you tie your self-worth to getting the right answer, every mistake feels like a character flaw.

You need to adopt the mindset of a Scientist:
- You are the Learning Process itself. You are the curiosity, the work ethic, the resilience.
- The Grade is just Data. It is simply the output of a single, specific experiment on a single specific day.
For example, if a Ferrari engine performs poorly because it had bad fuel, we don’t say the engine is trash. We say the input (fuel) was wrong. Similarly, if you fail a test, it doesn’t mean you are broken. It means your variables—your study habits, your sleep, your preparation—were off.

A bad grade is not your identity. It is guidance.

Breaking the Cycle

Ready to shift from being a “Grade Hunter” to a true “Learner”? Use these two simple techniques to pinpoint where you are in that transition and determine the necessary steps to move forward.

1. The “Two-Week Audit.”

I challenge you to a challenging experiment. Take a test you aced two weeks ago. Sit down and take it right now, without reviewing your notes.

The difference between your score then (95%) and your score now (55%) is your Fake (Lost) Knowledge. That 40-point gap represents wasted energy. It is time spent renting, not owning. If the gap is huge, your study method is broken, regardless of your GPA.

2. The Feynman Technique (The Ownership Test)

Physicist Richard Feynman had a simple rule for understanding, which he borrowed from Albert Einstein. To prove you have mastered a concept, you must be able to explain it in simple language, without jargon, to someone who has no background in the topic (like a smart 12-year-old).

If you can’t explain it simply, you don’t understand it. You have only memorized the definition. You are stuck at the bottom of Bloom’s Taxonomy.

The Bottom Line

The world is full of influencers and algorithms showing you the easy way to obtain a high test score on the ACT and achieve the most sought-after degrees, jobs, and accolades. Yet they rarely show you how to retain the knowledge required for long-term success.

Success in STEM requires three “old school” prerequisites that cannot be skipped: Curiosity, a Passion for Learning, and a Passion for Solving Problems.

If you have these, the grades will eventually follow. But more importantly, later in life, when the grades stop mattering, the expertise will remain.
January 4, 2026
The Impact of Calculators on Fundamental Math Skills
To follow up on my previous post, I cannot stress enough that four basic math skills: dimensional analysis, scientific notation, estimation, and significant figures – are prerequisites for anyone interested in math and sciences. Mastering these concepts helps stop the “operator headspace” mistakes that happen when you use your calculator as a crutch.

My biggest concern is that leaning too much on calculators is actually making students worse at fundamental math. For example, in the students I tutor, I’m seeing a drop in their ability to do mental math, a poor sense of estimation, and a failure to build that crucial “number sense” – that gut feeling about how numbers work and whether an answer makes any sense.

It’s a bit disappointing to me when I can perform math functions such as addition, subtraction, multiplication, division, and PEMDAS calculations faster and more accurately in my head than my students can on their fancy $100 calculator.

Therefore, the question I’m asking is:

“When kids let the calculator do the work, do they skip the mental practice needed to really lock in these vital skills?”

What Do the Experts Say?

Educational research points to a broader consensus: the impact of calculators isn’t automatically negative. The general feeling among experts is that when calculators are used correctly, they don’t inherently make students less capable at math. Instead, they suggest that any negative results usually come not from the calculator itself, but from using it poorly or too much. This often boils down to schools failing to have an intelligent, deliberate plan for when and how to bring this technology into the classroom. When the calculator becomes a crutch – used for problems students could easily do in their heads or on paper – that feared skill loss can definitely happen. But on the flip side, when they’re introduced as tools for digging into tougher concepts, checking answers, or handling the annoying arithmetic in advanced problem-solving, they can be helpful. They let students focus on deeper mathematical thinking and understanding.

How Should We Address These Concerns?

Math educators strongly advocate a structured, phased approach to the introduction of calculators:
- Prioritize Traditional Methods: Students must first be required to build a strong foundation in mathematics through traditional mental math and written arithmetic methods. This guarantees that these techniques and number sense are firmly established.
- Introduce Calculators as a Tool, Not a Replacement: Calculators should be introduced later in the elementary school years (not second grade), transitioning from an everyday practice to a valuable educational tool. Their primary function should be to support the student, not replace mental calculations.
- Introduce Calculators as a Resource for Checking Answers: Confirming answers acquired through mental or written technique.
- Introduce Calculators for Exploring Complex Numerical Systems: In secondary and post-secondary classrooms, calculators are introduced as a tool for investigating sequences or statistics on large data sets where calculation time is prohibitive.
- Introduce Calculators for Solving Conceptually Challenging Problems: Working with complex problems where the challenge lies in understanding the concept and setup, not in the basic arithmetic calculation itself.
This is an intelligent approach to introducing the calculator in the classroom, as it allows students to actively check their work. This is all about helping them master the calculations and truly understand how the math works. The goal here is to boost their learning, not get in the way of it.

High School and College STEM Courses: The Dangers of Calculator Over-Dependence

When you get to advanced math and science courses, relying too much on a calculator isn’t just about whether you can do the basic arithmetic (you should be able to); it’s about some more concerning issues. Specifically, whether using the calculator too often can affect your grasp of the concepts, make you rusty at solving problems algebraically, and weaken your crucial ability to estimate answers quickly to check your work.

Using powerful tools like TI graphing calculators can be a risk for learning. Certainly, these instruments make complex math operations simple, but that convenience can slow down a student’s development. Students who always simply punch numbers into their calculator to get an answer often miss out on building important “number sense.” This basic skill is key to quickly seeing if an answer is logical. Without it, students are more likely to accept completely wrong answers due to simple input errors because they haven’t developed the gut feeling that an answer is just plain wrong. Getting that immediate result skips the necessary learning steps of estimating and checking the math in your head.

Graphing calculators, while excellent tools that may assist a student’s understanding of the relationship between an algebraic equation and its graph, may also lead to over-reliance. When students rely too heavily on the calculator, they may be satisfied with merely seeing relationships – such as the curve’s shape or the location of an equation’s roots – without making the effort to understand the fundamental mathematical reasoning.

True mathematical mastery requires knowing not only what the graph looks like, but why it is structured that way. This deeper knowledge develops through hands-on engagement, not just by pressing buttons. The danger is that the calculator becomes a black box: it provides correct answers without explaining the logic behind the calculations, ultimately blocking the development of real mathematical understanding.

I must admit I am not a fan of the Ti-83/84 series of graphing calculators, perhaps because I have not used them as much as the students I‘ve tutored. I use the Ti-30 series for calculations, and for graphing functions, I use Desmos (www.Desmos.com), which I find to be a powerful tool that produces graphs I can easily manipulate and that are easier to see on my computer screen. I recommend it to every student I work with.

Personal Commentary

I believe it is crucial to learn how to evaluate a graph, a skill that goes beyond just plugging an equation into your graphing calculator and seeing the resulting graph on the screen. I had a Physics professor at Centre College, Dr. Marshall Wilt, who insisted that we learn how to graph and interpret the experimental data we obtained in the laboratory, as well as the relationships between small changes in inputs and the resulting output for equations such as the distance equation: ( $x_f=\;x_o+vt+at^2$ ). Albeit this was in the late 1970s, before graphing calculators were available, this was a skill that I used throughout my career.

Learning to evaluate graphs, regardless of how they are produced, and understanding the data they represent is a critical skill, useful, for example, on the ACT Science section, where graphical interpretation determines the correct answer.

Also, understanding graphical components such as slope and y-intercept is important for data interpretation, especially in chemistry, where they represent the reaction rate and the endpoints of a reaction.

From a Positive Perspective: How Calculators Help

Calculators are beneficial because they automate the long, repetitive mathematical calculations. This automation means you don’t have to waste time doing tedious work manually; for example, long division problems, complex multiplications, or solving big sets of equations.

The payoff? Students can focus their attention on bigger concepts. Instead of endless drills, the focus shifts to building higher-order thinking skills, figuring out the best way to tackle a problem, and really getting the math – like understanding of why a procedure works and when to use it. Basically, students can put their energy into setting up the problem, interpreting what the answer means, and grasping the core math ideas rather than getting bogged down in the steps of calculation itself.

Graphing calculators are great tools for exploring, questioning, and visualizing math concepts, turning complex equations into graphs. Students can quickly try out ideas and immediately see what happens when they tweak a function—like instantly watching how changing the numbers in a quadratic function ( $y=ax^2+bx+c$ ) shifts the parabola’s shape, direction, and peak. This fast, back-and-forth feedback encourages students to ask “what if?”, sparks their curiosity, and helps them really see the connection between the formula and the graph.

Calculators promote real-world data analysis skills. Restricting math problems to simple, whole numbers creates an artificial learning environment that fails to prepare students for the “messy” data they will encounter in professional fields such as science, finance, and engineering. Real-world applications invariably involve complex and irregular numbers. By using calculators, students can engage with authentic, complex data sets. This practice not only allows them to tackle applicable, practical problems that mirror professional scenarios but also reinforces the practical application of mathematics, thereby significantly boosting their skills in data interpretation and analysis.

Summary

The answer to my initial question:

“When kids let the calculator do the work, do they skip the mental practice needed to really lock in these vital skills?”

is complex. The expert consensus suggests the answer is no, not necessarily. The problem isn’t the calculator itself, but how it is used.

When a calculator is used too soon, as a replacement for mental math and estimation, it becomes a crutch for problems a student should solve independently. It clearly sidesteps the mental exercise required to master fundamental skills such as dimensional analysis, estimation, and significant figures.

The path forward is clear: a structured, phased approach to integrate this technology is essential.
- Foundation First: Students must first master fundamental arithmetic and algebraic manipulation using traditional methods. This ensures the critical development of number sense and the ability to estimate and check answers quickly.
- Calculators as Investigational Tools: Once the foundation is solid, the calculator changes from a potential crutch into a powerful tool for learning. It allows students to automate tedious calculations in advanced problems, freeing them to focus on setting up the problem, understanding the concept, how changes in variables affect the algebra, and interpreting results.
- Understanding the “Why”: For advanced topics, particularly in STEM, the goal is not just the correct answer, but mastering the math itself – understanding why the graph looks a certain way or why a procedure works. The graphing calculator can illustrate the relationship between algebraic equations and their graphs ( $y=ax^2+bx+c$ ), but it must be paired with a conceptual understanding beyond merely pressing buttons.
The goal is to develop mathematically proficient students capable of determining when to rely on mental calculation, when to use written methods, and when to employ a powerful device like a calculator. While the calculator is an essential instrument for today’s STEM students, it must serve as a secondary aid to mathematical reasoning, not a substitute for it.
December 14, 2025
Preventing “Operator Headspace” Errors in STEM Education
Doing good science relies upon building your conclusions on solid, trustworthy observations and data. But what happens when you substitute your own critical thinking with blind faith in your calculator? This is the core of the “operator headspace” error concept. The situation that occurs when students trust the calculated result without performing a validity test, leading to a series of undetected errors.

One of my concerns is that allowing students to use calculators too early—or requiring expensive ones later—will cause their fundamental math skills to weaken. However, most experts agree that calculators are not the obstacle to learning math. The true hazard lies in misusing them in the educational setting.

The issue isn’t the number-crunching technology itself; it’s our failure to equip students with the essential “thinking skills” required to use it correctly. We must emphasize when to employ mental math to boost speed and cultivate number sense, and when to reach for a calculator for complex problems to save time.

A quick assessment of your mental safety net: If a calculation yielded a speed of $2,000 \frac{ft}{sec}$ for a jogger, would you catch the error? To build this internal defense mechanism, you must master the core principles: Dimensional Analysis, Scientific Notation, Estimation, and Significant Figures. These are more than just exam topics; they serve as your personal safeguards to ensure your answers are mathematically sound, logically consistent with the real world, and scientifically precise.

Skills First: You Master It Before You Automate It.

The absolute most important step is making sure you have a solid grasp of basic arithmetic, number sense, and estimation long before calculators become your go-to for everything. A student who understands why a calculation is happening won’t rely blindly on the machine.

The Calculator is a Helper, Not a Brain Replacement.

When you hit high school and college, advanced calculators become a must for dealing with complex equations and large amounts of data. At this point, the focus shifts to equipping yourself with the mental defenses you need to spot input errors and verify the machine’s answer. These are the higher-level skills that turn the calculator into a productivity boost instead of a crutch:

Unit Tracking (Dimensional Analysis): Making sure to follow the units throughout a problem to confirm the final unit makes sense. It’s a great way to catch a blunder.

Building a strong intuition for how big or small numbers really are: Scientific Notation.

Estimation: Performing a fast, mental estimate before punching in the numbers. If the calculator spits out something wildly different, you know to check your work immediately.

Precision Rules (Significant Figures): Learning when and how to report answers so you don’t claim more accuracy than the original measurements allow—it’s a sign of scientific maturity.

Breaking Down the Skills

I. Dimensional Analysis

Dimensional Analysis is the key to error-free unit conversions. It operates on a simple principle: treat units like algebraic variables that must cancel out during multiplication or division. This is an immediate safeguard against the complex mistakes that arise when converting between different measurement systems (e.g., converting miles per hour to meters per second).
An incorrect final unit (e.g., calculating square feet when you need cubic feet for the volume of a $3$ dimensional object) is a certain sign that a conversion error occurred. It’s a proactive way to prevent errors and an effective tool for diagnosing exactly where a calculation went wrong.

The Golden Rule: Every conversion factor must equal 1. For example:

$1\;mile\;=\;\frac{1609\;meters}{1\;mile}$

Example 1

Convert $60\; miles\; per\; hour\; (mph)$ into $meters \;per\; second\ (\frac{m}{s}).$

We start with the known value and multiply by a chain of conversion factors, ensuring units cancel diagonally:

$60\;\frac{miles}{1\;hour}\;x\;\frac{1609\;meters}{1\;mile}\;x\;\frac{1\;hour}{60\;minutes}\;x\;\frac{1\;minute}{60\;seconds}\;=\;X\;\frac{meters}{second}$

The calculation then becomes:

II. Scientific Notation

Scientific Notation is the indispensable tool for understanding the magnitude of a number at a glance. By expressing a number as a coefficient multiplied by a power of ten ( $A \times 10^B$ ), it instantly reveals the number’s true magnitude—its actual size. The exponent ( $B$ ) gives an immediate order-of-magnitude check, eliminating the complex demand for counting zeros.

This system protects against two common errors: mistyping the number of zeros (e.g., $0.0001$ instead of $0.001$ ) and losing perspective on the number’s scale during long calculations. Seeing $1.42\;x\;10^{-4}$ immediately communicates its small size, which is far clearer than counting a long string of leading zeros.

The calculator’s exponent function ( $\times 10^x$ or EE) is a safety mechanism against inputting long strings of zeros incorrectly. also streamlines the multiplication and division of huge and tiny numbers, making estimation easier.

Another bonus of using scientific notation, is that the value of $A$ is always <math data-latex="1\;\frac{<}{=}\;A1<=A<101\;\frac{<}{=}\;A<10. Which simplifies the division or multiplication of very large or small numbers. allowing you to very easily estimate the results.

For Example:

Using the Law of Exponents, to divide two numbers in scientific notation form:

$\frac{6.2×10^5}{3.3×10^3}\;=\;\frac{6.2}{3.3}\;x\;10^{5-3}\;estimating:\;\frac {6}{3}\;X\;10^{5-3}\;=\;2\;x\;10^2$

This type of manipulation of large and small numbers and the use of estimations will allow you to closely approximate the value to expect from your calculator. And, on multiple choice, timed exams (I.e. ACT, SAT), gives you an advantage, allowing you not to be dependent on using your calculator on these types of calculations at all.

III. Estimation

Estimation is arguably the most vital practice for combating “operator headspace errors,” and is the ultimate defense against absurd results. It involves performing a rapid, rough calculation—either mentally or on scratch paper—to determine the approximate range for the correct answer before running the precise, final calculation.

Estimation serves as a personal warning bell for:

Dumb Data Entry: It flags typos or misplaced decimal points that make the final answer ten, a hundred, or a thousand times too large or too small.

Crazy Results: If your calculation suggests a baseball is moving at $50,000 \;meters\; per\; second \;(\frac{m}{s})$ , your estimate should instantly scream, “Impossible!” and prompt you to re-check your entire process.

IV. Significant Figures

Significant Figures are the foundation of scientific honesty in measuring the precision of a measurement. Every instrument has limits; a ruler marked only in millimeters cannot yield a micrometer measurement. Significant figures ensure that your calculated answer never claims a higher level of precision than the least precise measurement used in the initial data set.

Significant figure rules prevent the final answer from misleadingly implying high precision. If your calculator displays $12.34567 \;(7\; significant\; figures)$ , but the least precise input you used had only $3\; significant\;figures\;(e.g., \;4.50)$ , you must round the result to match that lowest value $(i.e., 12.3)$ . This practice accurately communicates the reliability and uncertainty inherent in experimental data.

Summary

We’ve established that Estimation and Dimensional Analysis are the non-negotiable mental defenses you must learn to employ before committing to a calculation. These protocols are your barrier against operator headspace errors. However, the widespread introduction and mandatory use of powerful calculators—from simple four-function models in grade school to the advanced TI-series in college science and engineering—raises a critical and timely question:

“Does our reliance on these powerful tools effectively eliminate the very mental skills we’ve just deemed essential? ”

In my next post, I will address the concerns surrounding the appropriate use of calculators in the classroom to ensure the tool aids, rather than undermines, your scientific integrity.
December 7, 2025
Mastering STEM: 3 Keys to Success Beyond ‘Natural Genius’
There’s a persistent myth in Science, Technology, Engineering, and Mathematics (STEM): that success belongs to the “natural genius,” the person who just “gets it.”

Here’s the truth: Achieving mastery in challenging STEM fields has little to do with some magical, intrinsic gift. It is 100% based on the application of several advanced intellectual and behavioral strategies. Think of it as a complete operating system upgrade for your brain.

To move beyond the daily struggles and achieve genuine mastery in STEM, you need to commit to these three non-negotiable principles.

The Power of Modeling

Social Learning Theory, pioneered by Albert Bandura, shows that a huge part of human learning happens through observing and imitating others. But success isn’t about emulation (or copying) a single skill; it’s about modeling a complete system.

To succeed, you must actively observe and adopt the entire package of skills and habits from those who have already achieved high levels of success. For example:
- Advanced Technical Skills: How do experts and mentors break down a complex problem? Learn their analytical approaches.
- Powerful Work Ethic: Look at how they meticulously structure their study schedules, their uncompromising standards for quality, and their consistent effort.
- Powerful, Positive Mindset: How do they view failure? It’s purely objective, instructive data—nothing more.
Take action, stop focusing solely on the textbook content. Start noting the process of your most successful peers or mentors. How do they organize? When and how do they study? How do they handle a major setback? You want to copy and implement a system, not just learn content knowledge.

Escaping the “Developmental Trap.”

A massive barrier to our progress is what is called the “developmental trap.” This is when you inadvertently become rooted in ineffective behavioral patterns that feel comfortable but sabotage your future.

Are you chronically procrastinating? Do you find fault in everything you do, seeing only the negative outcomes, which paralyzes you from even starting? Are you habitually unclear about your goals and intentions, or vague in your communication with your fellow students/teachers/professors? These are self-sabotaging habits.

To break free, you must perform a conscious, honest self-assessment and start developing and exercising your self-awareness skills.

Follow-up on your self-assessment by:
- Installing these productive habits: Resilience (bouncing back from setbacks with renewed effort) and a rigorous work ethic (getting things done with uncompromising quality and efficiency).
- Discard low-return behaviors: Self-incrimination, self-doubt, and negativity.
Over time, your relentless effort will help create a powerful “internal compass.” Your motivation shifts from the temporary need for external validation (a good grade, a compliment) to an intrinsic drive—a non-negotiable, standard you’ve set for quality and thoroughness that you must meet, regardless of what anyone else thinks.

Prioritize the Process Over the Score

The final, and perhaps most crucial, mental adjustment is letting go of the destructive notion that you must achieve absolute, flaw-free perfection. That ideal is unattainable and will only lead to burnout.

The successful STEM student must value the process of learning and discovery over the final numerical score or grade.

When an experiment fails, a line of code breaks, or you get a subpar result on a quiz, how you react must change. Don’t view it as a “mess-up” or that you don’t have what it takes to “make it.” Instead, you must treat it as a starting point from which you learn and progress.

This data is essential for:
1. Precisely identifying your weaknesses.
2. Fine-tuning your approach to solving the problem or issue.
3. Educating you for the design of your future, a more refined attempt.
This mental shift is life-changing. It moves your focus from avoiding mistakes (a fear-based approach) to maximizing learning effectiveness (a growth-based approach.)

Summary

In the demanding world of STEM, setbacks—from experimental failures to complex problem-solving roadblocks and challenging coursework—are a daily certainty. Therefore, the single most critical factor for your long-term success and ultimate perseverance is your ability to effectively manage and recalibrate your expectations.

Really successful STEM students ditch the idea that they have to be absolutely perfect. They focus more on consistently putting in the hard work and sticking closely to the process (understanding the “why” and the “how”), instead of getting hung up on immediate, flawless results. This mindset change is a huge win: it means they stop seeing mistakes as a huge personal flaw and start seeing them as valuable, objective data—the stuff you need for real learning, figuring out new strategies, and improving down the line. In the end, this shift turns anxiety into a powerful tool for growth.
November 30, 2025
Essential Skills for Success in STEM: Initiative, Resolve, Perseverance, Resilience

You may be doing well in your math and science courses, or perhaps you’re already interested in areas such as computer programming, robotics, or video game design. While a passion for STEM and strong academic performance are certainly vital, true success in these fields requires more than just intelligence.

The key drivers—the qualities that will propel you through challenging projects, demanding courses, and even career setbacks—are the four absolutely vital tools in your personal growth toolkit for anyone charting a course in STEM: Initiative, Resolve, Perseverance, and Resilience.

What is Initiative, Resolve, Perseverance, and Resilience?

1. Initiative

What it is: The ability to self-start, take action without being told, and seek out new opportunities or skills.

Why it matters in STEM: The STEM fields are constantly evolving. What you learn today may be outdated in five years. Initiative is crucial for lifelong learning—the willingness to constantly teach yourself new skills (computer programming, robotics, advanced data analysis, or new analytical instrumentation) to remain current and competitive in the industry.

When performing research or problem-solving, it takes initiative to troubleshoot errors, design a better experiment, or learn to use a new piece of equipment before it’s required. It’s what drives you to excel.

Example: Your Chemistry professor assigns an open-ended laboratory project. The explicit expectation is a successful, unique final product. You must show the initiative to search for resources, organize the necessary equipment and reagents, and learn to operate the necessary tools needed to complete the project because the assignment demands it, not just because you feel like it.

2. Resolve

What it is: A firm determination to achieve a specific goal, resisting distractions, and maintaining focus even when things get tough. The unwavering focus needed to complete a difficult project, solve a complex equation, or commit to the years of study required for a specialized field of study.

Why it matters in STEM: STEM fields demand long-term commitment. Resolve is what helps you stay committed to completing that difficult assignment, even when exhaustion hits. Push through a difficult physics derivation, knowing the understanding will unlock new perspectives. See past a frustrating semester or a challenging first-year chemistry, physics, or math course, reminding you of your ultimate career aspirations. It’s the inner conviction that keeps you on track.

Example: Introductory college courses, such as Organic Chemistry, Physics, and Calculus, are often intentionally challenging to test your preparedness to succeed in upper level courses. When faced with a low grade, resolve is the quality that prevents you from abandoning your major. Initiative is the drive to seek out help by finding a tutor, joining a study group, or meeting with the professor to grasp the material you do not understand, instead of simply giving up.

3. Perseverance

What it is: The sustained effort to keep working despite difficulties, serving as the dedication required to solve tough problems through hours of calculations, research, or repeated experiments. It’s the long-term, consistent effort.

Why it matters in STEM: STEM is rarely a straight line to success. Perseverance means spending countless hours debugging computer programming, even when you’re convinced it’s flawless. Re-running an experiment five times because you’re confident there’s a pattern you’re missing. Staying up late to understand a complex mathematical concept until it finally clicks.

Example: You struggle with a Chemistry laboratory assignment and are tempted to give up. Your instructor intervenes, not by giving you the answer, but by offering a small suggestion, confirming the difficulty of the task, and requiring you to follow up in an hour. This structured support prevents you from feeling abandoned in your efforts, reinforces the importance of struggle, and teaches you the value of perseverance.

While the ultimate decision to continue is yours, external factors, the support from your instructor, are essential. The setting of an expectation, the modelling of how to continue in the process, and the structured support act as powerful motivations, transforming your ability to just keep going into an established, automatic behavior (perseverance).

4. Resilience

What it is: The capacity to recover quickly from setbacks, disappointments, or outright failures, viewing setbacks not as defining moments but as valuable data and learning opportunities.

Why it matters in STEM: Failure isn’t a setback in STEM; it’s a feature. Scientific discovery often involves many “failed” experiments before a breakthrough. Resilience allows you to: bounce back from a low test score, analyze what went wrong, and adjust your study habits.

Example: It can be challenging for you to picture what “resilience” looks like. Mentors provide a crucial model. When you witness your research advisor’s experiment fail, and instead of getting discouraged, your advisor calmly analyzes the data, identifies the potential sources of error, and immediately starts correcting the issues for the next trial run. These actions model resilience and teaches you how to respond appropriately to setbacks.

STEM fields are characterized by constant challenges and an emphasis on complex problem-solving. Success relies less on your natural talent and more on your willingness to engage in a productive learning process. And that success rarely comes on the first try. It is common for an experiment to produce unexpected results or a mathematical proof to contain an error. Instead of seeing these setbacks as personal shortcomings, students need the mindsets of resilience and perseverance to see a failure as a starting point.

Is Initiative, Resolve, Perseverance, and Resilience a Personality Trait or a Learned Skill?

Initiative, resolve, perseverance, and resilience are generally understood as learned behaviors. Psychologists like Carol Dweck argue that these qualities stem from a Growth Mindset—the belief that our abilities and intelligence can be developed, rather than a fixed personality trait. While some people might appear naturally more determined to manage and learn from their struggles, everyone has the capacity to develop these essential skills.

Think of initiative, resolve, perseverance, and resilience as learned skills that, when practiced consistently, become an integral, defining part of your character or personality. For a STEM student, it is critical to recognize the value in treating them as skills that require deliberate practice.

The Power of Role Models, Mentors, and External Expectations

The skills of initiative, resolve, perseverance, and resilience isn’t something you can achieve entirely on your own, however you can always begin the process. The most effective and the smoothest path to growth in these areas requires external guidance. Role models, mentors, and the right external expectations act as a vital catalyst in forging these qualities.

How do role models, mentors, and external expectations cultivate these critical skills? Here are four key examples:

Observation: Professors, Mentors, and Role Models provide critical “how-to” knowledge. Observing an experienced chemist handle an instrument failure calmly or a scientist gracefully accept and learn from a failed experiment offers a real-world demonstration of resilience and perseverance in action.

Accountability: External expectations, whether it is from a professor, mentor, or a course syllabus, establish defined goals and deadlines that require action. Taking on a challenging project with its external pressures, its deadlines and reporting requirements, serves as a catalyst. It triggers the initiative needed to start and, crucially, builds the internal resolve and strength required for sustained effort toward completion.

A Defined Strategy for Success: Effective teachers and mentors avoid simply giving answers. Instead, they offer focused, constructive feedback, guide individuals through roadblocks, and recognize small achievements. This strategic support reinforces successful behaviors, driving long-term competence and success.

Reinforcement and Feedback: These critical skills are only learned effectively when you receive balanced feedback from your professors and mentors, parents as well – positive reinforcement when you suceed and constructive criticism when you fall short.

A Strategy for Your Personal Growth and Success

As you navigate your academic life and plan for a career in science, technology, engineering, or math, your focus must extend beyond formulas and facts. You need to actively look for opportunities to develop your initiative, resolve, perseverance, and resilience. So take action with the following approach:

1. Embrace the Hard Stuff: Never shy away from difficult assignments or complex projects. Challenges are opportunities in disguise.

2. Treat Failures as Data: Every setback is not an end, but a valuable data point. Analyze what went wrong and adjust your approach.

3. Actively Seek Mentors: Find someone whose approach to challenges inspires you, and commit to learning from their wisdom and experience.

4. Practice Self-Reflection: When things get tough, take a moment to ask yourself: How did I react? What could I do differently next time?

Conclusion

These qualities are not just career buzzwords; they are the foundation of personal growth and the essential fuel for scientific discovery and innovation. The combination of strong grades and these four psychological attributes is what ultimately separates a good student from future success in their career path, capable of making a difference in a STEM field. Cultivate them, and you will do more than just succeed in STEM; you will thrive in every aspect of your life.

November 19, 2025
Beyond the Textbook: Why Critical Thinking is Your Ultimate STEM Skill

As a STEM student, you’re constantly immersed in data, complex equations, and technical concepts. You’ve known and mastered the Scientific Method—observing, hypothesizing, experimenting, and concluding—but that structured process is only half the battle. The other, perhaps more crucial, half is Critical Thinking. While the Scientific Method is a rigid framework for inquiry, critical thinking is the flexible process that drives it. It’s the difference between merely memorizing a formula and truly understanding its foundations and limitations. For you, this means going beyond rote learning to actively and skillfully analyze, synthesize, and evaluate the information you encounter in the lab, the lecture hall, and the world around you.

This analytical mindset comprises several core skills essential to your future, regardless of which career path you choose..

First, you must develop a relentless habit of questioning information. Don’t just question external sources; turn that rigorous examination onto your own work. You must constantly ask: Is this data truly reproducible? Are my initial assumptions that led to this result reliable? This internal skepticism is key.

Second, the ability to perform careful error analysis is primary. This means moving past simply reporting a “failed” test and instead recognizing the subtle flaws in your experimental design, data collection methods, or calculations. Master the ability to identify the sources of error in your experiment. This isn’t about placing the blame on yourself or others; it’s about learning and improving.

Third, you must effectively evaluate information sources. When researching a project, learn to distinguish sound, evidence-based conclusions from claims based upon false assumptions or bias. This skill is vital when designing an experiment or reading specialized technical literature.

Real-world Example: Evaluating an Information Source

A thoughtful, analytical evaluation of an Information source serves as an excellent example of applying this critical evaluation skill—essential for navigating the complex media environment today. All too frequently, we accept what we encounter online or on message boards as fact. Regardless of whether we agree with the content or not, we rarely take the time to determine its validity. This requires a rigorous assessment of the information’s credibility, accuracy, and fairness.

Your process begins with understanding who the source is; this means performing quick additional research to assess who created the content, including the purpose behind the creation of the content and any editorial bias, while verifying the author’s expertise. Highly sensational headlines or anonymity should immediately raise your suspicion.

Next, shift your focus to fact-checking the content itself. Examine the quality of evidence, looking specifically for hard data, statistics with cited methodologies, and primary sources, while simultaneously checking the language for emotional arguments or wording that signals an intent to persuade or distract you intentionally, versus simply reporting objectively.

Finally, your evaluation must thoroughly assess the argument’s fairness and completeness. This means checking that the source acknowledges and fairly represents opposing viewpoints, offers criticized parties a chance to respond or rebut the information or opinion, and avoids relying on unstated, implied assumptions.

Ultimately, this comprehensive process moves you beyond merely accepting the Information as fact, leading you to an informed decision about the material’s actual validity and practical usefulness.

Conclusion

Critical thinking is the key factor that elevates a capable STEM student into an innovative and successful scientist or engineer. It’s the powerful mechanism that allows you to process complex, unstructured data, recognize underlying patterns, and formulate valid logical conclusions where standard solutions may not exist. This skill deepens comprehension and improves retention, translating theoretical concepts into practical, usable knowledge for your future development.

I strongly urge you to cultivate your expertise in challenging assumptions, analyzing evidence, and applying logical reasoning now. By doing so, you position yourself as an active contributor in your field, not merely a passive learner and recipient of information. As the volume of data and pace of technology accelerate, remember this lasting truth: your most indispensable tool for lifelong learning and effective problem-solving isn’t the newest gadget or a sophisticated piece of machinery. It is your inherent capacity to think in an evidence-based, exact, and open-minded manner.

November 16, 2025
Why Do I Have to Learn This? I’ll Never Use It.

By our very nature, we are inquisitive – always asking “why?”; usually in response to being asked or told to do something. Have you ever asked the question:“Why do I have to learn this? Or, “Why do I have to do this?” I’ll never use it.” I know I did, more than once. Rarely are you given a reason why it is essential to understand the information presented in your high school or college courses and how it relates to what you want to accomplish in life. Sometimes, the answer is simple: you need to know it for the next test. But other times, there are deeper reasons. For example, learning about history can help us understand the present. Learning about science helps us make informed decisions about the world around us and how systems work together. And learning math teaches us to think logically and solve problems in our everyday lives.

Speaking from experience, there is a great deal of information taught in your math and science classrooms, the facts, figures, formulas, dates, and names, you will never use again – whether you intend to go to college or not. And don’t think you will stop asking this question once you decide on your career path – there will always be a training session you don’t want to attend, with more information you don’t see as being vital to you doing your job. It’s a never-ending cycle. What if I told you that the challenges and struggles you face in your classes, more than content knowledge, are vital to your overall growth as a student and will positively impact your success in any career you choose? Content knowledge measured by test scores and grades may or may not be your ultimate objective; that depends on your priorities. I believe what’s truly important and what we sometimes fail to realize is that the “process of learning” equips us with the “tools” for our success.

May 28, 2025